Dans cette serie d’articles sur les algorithmes génétiques, j’ai employé le terme extremum local à plusieurs reprises sans jamais vraiment l’expliquer.

Pour comprendre ce qu’est un extremum local, on va se servir d’une fonction mathématique. Rassurez-vous on ne va pas faire de math, je vais juste me servir du visuel. Imaginons la fonction f(x) suivante:

Admettons que la fonction f soit notre fonction d’évaluation. Dans ce cas chaque x représente un chromosome parmi tous ceux possibles. Et à chaque valeur x correspond une valeur y qui serait notre score.

Nous voulons connaitre la valeur de x qui maximise la fonction, qui donne le plus grand y/score possible. Comment faire ? Le plus simple est de balayer toutes les valeurs possibles de x, soit calculer f(0), f(1), f(2), etc. Une fois tout ça calculé, on sait quel x donne le plus grand y. Où est le problème ? Imaginons que x puisse prendre comme valeur les nombres entiers de zéro à un milliard, imaginons aussi que la fonction d’évaluation (f) soit un peu longue et prenne 1 seconde de calcul. Ça veut dire qu’il faudra (à la louche) 11820 jours pour balayer toutes les valeurs de x. Pas possible, faut trouver autre chose.

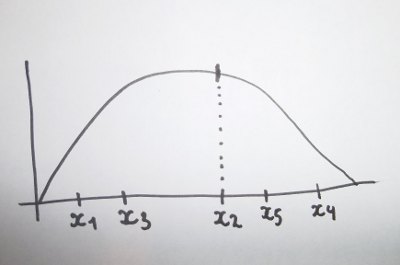
Les algorithmes génétiques, et plus largement les algorithmes stochastiques, utilisent en partie le hasard pour résoudre ce type de problème. La solution la plus simple est d’évaluer des valeurs de x tirées au hasard. Plus on disposera de temps, et plus on s’approchera théoriquement de la valeur maximum (l’extremum). La figure suivante propose cinq valeurs de x au hasard. Un premier hic, c’est que pour obtenir l’extremum en un temps raisonnable, il faut avoir beaucoup de chance. Un second hic, c’est que pour être sûr d’obtenir l’extremum il faut toujours balayer toutes les possibilités.

Une solution plus intelligente est de tirer une première valeur de x au hasard. Puis on ajoute une petite valeur à x, par exemple 1, 5, 10 ou 100 suivant l’étendue des x possibles. On a donc x1 = x + 1. Si le nouveau y obtenu est plus grand que l’ancien on est sur la bonne voie, sinon on retranche cette petite valeur (x2 = x - 1). En progressant ainsi par petits bonds, on arrivera à l’extremum.

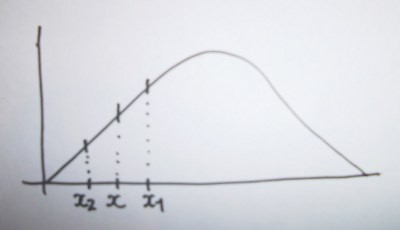
Cette progression par petits bonds est assez proche, dans l’idée, de la mecanique des algorithmes génétiques. En ajustant comme il faut la petite valeur qu’on ajoute aux x successifs, on obtiendra l’extremum en un temps raisonnable.

Edit du 1 oct 2013 Cette petite valeur ajoutée à x peut-être considérée comme une mutation.

Alors où est le problème maintenant ? Pour le visualiser il faut changer de fonction mathématique:

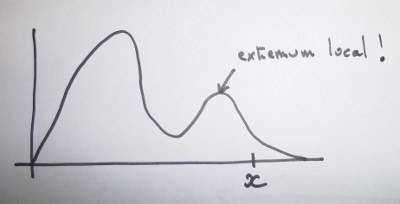
Si on n’a pas de chance, on va tirer au hasard une première valeur de x qui nous emmènera immanquablement vers un extremum local, et non pas vers l’extremum global !

Voilà, j’espère que cette petite démonstration a remplie son office et que vous visualisez maintenant clairement cette histoire d’extremum local.

À demain.